Локальная теорема Муавра — Лапласа

С ростом n форма биномиальной фигуры распределения становится похожа на плавную кривую Гаусса.

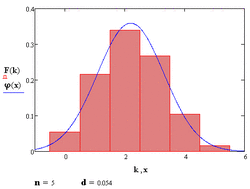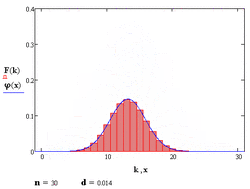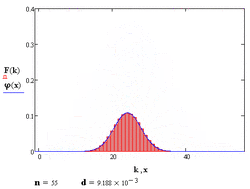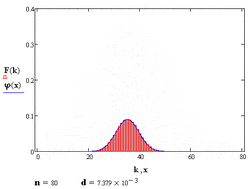
Теорема Муавра — Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Теорема Муавра-Лапласа является частным случаем центральной предельной теоремы.

Если при каждом из [math]\displaystyle{ n }[/math] независимых испытаний вероятность появления некоторого случайного события [math]\displaystyle{ E }[/math] равна [math]\displaystyle{ p \in (0, 1) }[/math], и [math]\displaystyle{ m }[/math] — число испытаний, в которых [math]\displaystyle{ E }[/math] фактически наступает, то вероятность справедливости неравенства близка (при больших [math]\displaystyle{ n }[/math]) к значению интеграла Лапласа.

Применение

При рассмотрении количества [math]\displaystyle{ m }[/math] появлений события [math]\displaystyle{ A }[/math] в [math]\displaystyle{ n }[/math] испытаниях Бернулли чаще всего нужно найти вероятность того, что [math]\displaystyle{ m }[/math] заключено между некоторыми значениями [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math]. Так как при достаточно больших [math]\displaystyle{ n }[/math] промежуток [math]\displaystyle{ [a, b] }[/math] содержит большое число единиц, то непосредственное использование биномиального распределения

[math]\displaystyle{ p_n(m)=\frac{n!}{m!(n - m)!}p^mq^{n-m} }[/math]

требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей.

Поэтому используют асимптотическое выражение для биномиального распределения при условии, что [math]\displaystyle{ p }[/math] фиксировано, а [math]\displaystyle{ n\rightarrow+\infty }[/math]. Теорема Муавра — Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция. Формула теоремы Муавра — Лапласа применяется при больших [math]\displaystyle{ n }[/math] и [math]\displaystyle{ m }[/math]. Теорема Муавра — Лапласа будет тем точнее, чем ближе [math]\displaystyle{ p }[/math] к [math]\displaystyle{ 1/2 }[/math]. При [math]\displaystyle{ p }[/math] близком к [math]\displaystyle{ 0 }[/math] или [math]\displaystyle{ 1 }[/math] формула теоремы Муавра — Лапласа дает большую погрешность.

Формулировка

Если в схеме Бернулли [math]\displaystyle{ n }[/math] стремится к бесконечности, то для [math]\displaystyle{ m }[/math] в окрестности [math]\displaystyle{ np }[/math] мы можем исходить из апроксимации

[math]\displaystyle{ {n \choose m}\, p^m q^{n-m} \simeq \frac{1}{\sqrt{2 \pi npq}}\,e^{-\frac{(m-np)^2}{2npq}}, \qquad p+q=1,\ p, q \gt 0 }[/math]

в том смысле, что отношение левой стороны равенства к правой стороне стремится к [math]\displaystyle{ 1 }[/math] если [math]\displaystyle{ n → ∞ }[/math].

Таким образом, если в схеме Бернулли [math]\displaystyle{ n }[/math] стремится к бесконечности, величина [math]\displaystyle{ p \in (0, 1) }[/math] постоянна, а величина [math]\displaystyle{ x_m = \frac{m - np}{\sqrt{npq}} }[/math] ограничена равномерно по [math]\displaystyle{ m }[/math] и [math]\displaystyle{ n }[/math] (то есть [math]\displaystyle{ \exists a, b: -\infty \lt a \leqslant x_m \leqslant b \lt +\infty }[/math]), то

[math]\displaystyle{ P_n(m) = \frac{1}{\sqrt{2\pi npq}}\exp\left(-\frac{x_m^2}{2}\right)(1 + \alpha_n(m)) }[/math]

где [math]\displaystyle{ \left| \alpha_n(m) \right| \lt \frac{c}{\sqrt{n}}, c=\text{const} \gt 0 }[/math].

Приближённую формулу

[math]\displaystyle{ P_n(m) \approx \frac{1}{\sqrt{2\pi npq}}\exp\left(-\frac{x_m^2}{2}\right) }[/math]

рекомендуется применять при [math]\displaystyle{ n \gt 100 }[/math] и при [math]\displaystyle{ m \gt 20 }[/math].

Абсолютная погрешность формулы теоремы имеет порядок [math]\displaystyle{ 1/\sqrt {n} }[/math].

Доказательство

Для доказательства теоремы будем использовать формулу Стирлинга из математического анализа:

[math]\displaystyle{ s!=\sqrt{2\pi}s^{s+1/2}e^{-s}e^{\theta_s}, }[/math] (1)

где [math]\displaystyle{ 0\lt \theta_s\lt 1/{12s} }[/math].

При больших [math]\displaystyle{ s }[/math] величина [math]\displaystyle{ \theta }[/math] очень мала, и приближённая формула Стирлинга, записанная в простом виде

[math]\displaystyle{ s!=\sqrt{2\pi}s^{s+1/2}e^{-s} }[/math] (2)

даёт малую относительную ошибку, быстро стремящуюся к нулю при [math]\displaystyle{ s\rightarrow+\infty }[/math].

Нас будут интересовать значения [math]\displaystyle{ m }[/math], не очень отличающиеся от наивероятнейшего. Тогда при фиксированном [math]\displaystyle{ p }[/math] условие [math]\displaystyle{ n\rightarrow+\infty }[/math] будет также означать, что

[math]\displaystyle{ m\rightarrow+\infty, n-m\rightarrow+\infty. }[/math] (3)

Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем

[math]\displaystyle{ p_n(m)\approx\sqrt{\frac{n}{2\pi m(n-m)}}\left(\frac{np}{m}\right)^{m}\left(\frac{nq}{n-m}\right)^{n-m}. }[/math] (4)

Также понадобится использование отклонения относительной частоты от наивероятнейшего значения:

[math]\displaystyle{ x_m=\frac{m}{n}-p. }[/math] (5)

Тогда выражение (4) приобретает вид:

[math]\displaystyle{ p_n(m)=\left[2\pi n(p+x_m)(q-x_m)\right]^{-1/2}\left(1+\frac{x_m}{p}\right)^{-n(p+x_m)}\left(1-\frac{x_m}{q}\right)^{-n(q-x_m)}. }[/math] (6)

Предположим, что

[math]\displaystyle{ x_m\lt pq. }[/math] (7)

Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора:

[math]\displaystyle{ -n\left[(p+x_m)\ln{\left(1+\frac{x_m}{p}\right)} + (q-x_m)\ln{\left(1-\frac{x_m}{q}\right)}\right]= }[/math]

[math]\displaystyle{ -n\left[(p+x_m)\left(\frac{x_m}{p}-\frac{x_m^2}{2p^2}+\frac{x_m^3}{3p^3}-\cdots\right)+(q-x_m)\left(-\frac{x_m}{q}-\frac{x_m^2}{2q^2}-\frac{x_m^3}{3q^3}-\cdots\right)\right]. }[/math] (8)

Располагаем члены этого разложения по степеням [math]\displaystyle{ x_m }[/math]:

[math]\displaystyle{ -n\left[\frac{x_m^2}{2}\left(\frac{1}{p}+\frac{1}{q}\right)-\frac{x_m^3}{6}\left(\frac{1}{p^2}-\frac{1}{q^2}\right)+\cdots\right]. }[/math] (9)

Предположим, что при [math]\displaystyle{ n\rightarrow+\infty, }[/math]

[math]\displaystyle{ nx_m^3\rightarrow 0. }[/math] (10)

Это условие, как уже было указано выше, означает, что рассматриваются значения [math]\displaystyle{ m }[/math] не очень далёкие от наивероятнейшего. Очевидно, что (10) обеспечивает выполнение (7) и (3).

Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен

[math]\displaystyle{ -\frac{n}{2pq}x_m^2. }[/math] (11)

Отбрасывая малые слагаемые в скобках первого множителя (6), получаем

[math]\displaystyle{ p_n(m)\approx\left(\frac{1}{\sqrt{2\pi npq}}\right)\exp{\left(-\frac{n}{2pq}x_m^2\right)}. }[/math] (12)

Обозначив

[math]\displaystyle{ \sigma=\sqrt{\frac{pq}{n}}, }[/math] (13)

переписываем (12) в виде

[math]\displaystyle{ p_n(m)\approx\frac{1}{n}\frac{1}{\sigma\sqrt{2\pi}}\exp{\left(-\frac{x_m^2}{2\sigma^2}\right)}=\frac{1}{n}\varphi(x_m), }[/math] (14)

Где [math]\displaystyle{ \varphi(x_m) }[/math] — нормальная функция.

Поскольку в интервале [math]\displaystyle{ [m,m+1) }[/math] имеется только одно целое число [math]\displaystyle{ m }[/math], то можно сказать, что [math]\displaystyle{ p_n(m) }[/math] есть вероятность попадания [math]\displaystyle{ m }[/math] в интервал [math]\displaystyle{ [m,m+1) }[/math]. Из (5) следует, что изменению [math]\displaystyle{ m }[/math] на 1 соответствует изменение [math]\displaystyle{ x_m }[/math] на

[math]\displaystyle{ \Delta x=\frac{1}{n}. }[/math] (15)

Поэтому вероятность попадания [math]\displaystyle{ m }[/math] в интервал [math]\displaystyle{ [m,m+1) }[/math] равна вероятности попадания [math]\displaystyle{ x_m }[/math] в промежуток [math]\displaystyle{ [x_{m0},x_{m0} + \Delta x), }[/math]

[math]\displaystyle{ P(x_{m0} \le x_m \le x_{m0} + \Delta x) = \varphi(x_m)\Delta x. }[/math] (16)

Если [math]\displaystyle{ n\rightarrow+\infty }[/math], то [math]\displaystyle{ \Delta x\rightarrow+0 }[/math] и равенство (16) показывает, что нормальная функция [math]\displaystyle{ \varphi(x) }[/math] является плотностью случайной переменной [math]\displaystyle{ x_m }[/math].

Таким образом, если [math]\displaystyle{ n\rightarrow+\infty, nx^3\rightarrow0 }[/math] то для отклонения относительной частоты от наивероятнейшего значения справедлива асимптотическая формула (16), в которой [math]\displaystyle{ \varphi(x) }[/math] — нормальная функция с [math]\displaystyle{ x_m=0 }[/math] и [math]\displaystyle{ \sigma^2=\frac{pq}{n} }[/math].

Таким образом, теорема доказана.

Литература

• Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005
• Ширяев А. Н. Вероятность, — М.: Наука. 1989.
• Чистяков В. П. Курс теории вероятностей, — М., 1982.